2.1 Measurement Precision

Workshop: “Handling Uncertainty in your Data”

Dr. Mario Reutter & Juli Nagel

What is (Measurement) Precision?

Interest Group: Open and Reproducible Research (IGOR)

Part of the German Reproducibility Network:
https://www.youtube.com/watch?v=sQFmB_EY1PQ

Group-level Precision

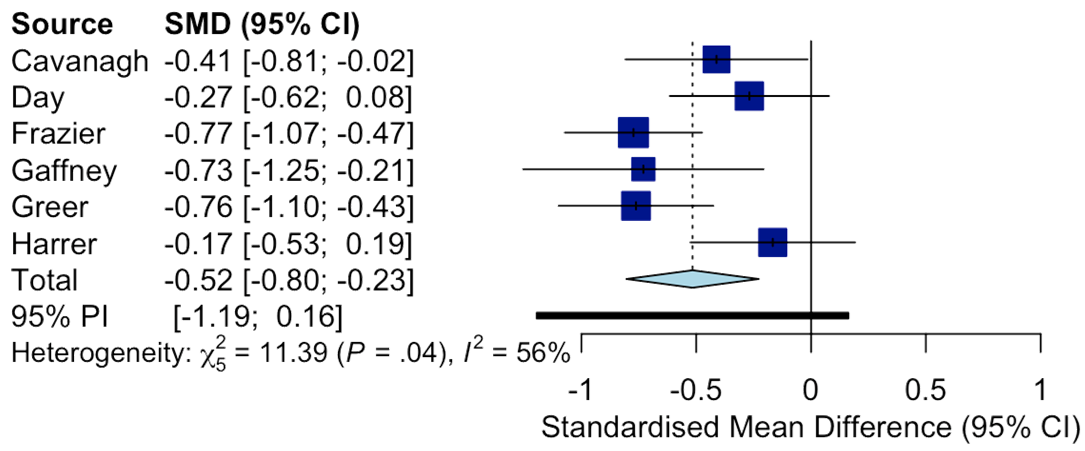
https://bookdown.org/MathiasHarrer/Doing_Meta_Analysis_in_R/forest.html#forest-R

→ Effects in relation to their group-level precision

Group-level Precision 2

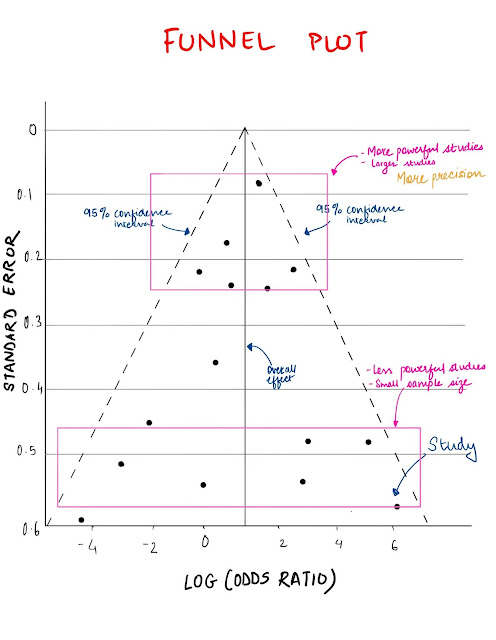
https://www.medicowesome.com/2020/04/funnel-plot.html

→ Effects in relation to their group-level precision

What is Precision?

1. Precision is indicated by errorbars / confidence intervals

Subject-Level Precision

Is there a meaningful correlation?

Subject-Level Precision 2

Is there a meaningful correlation?

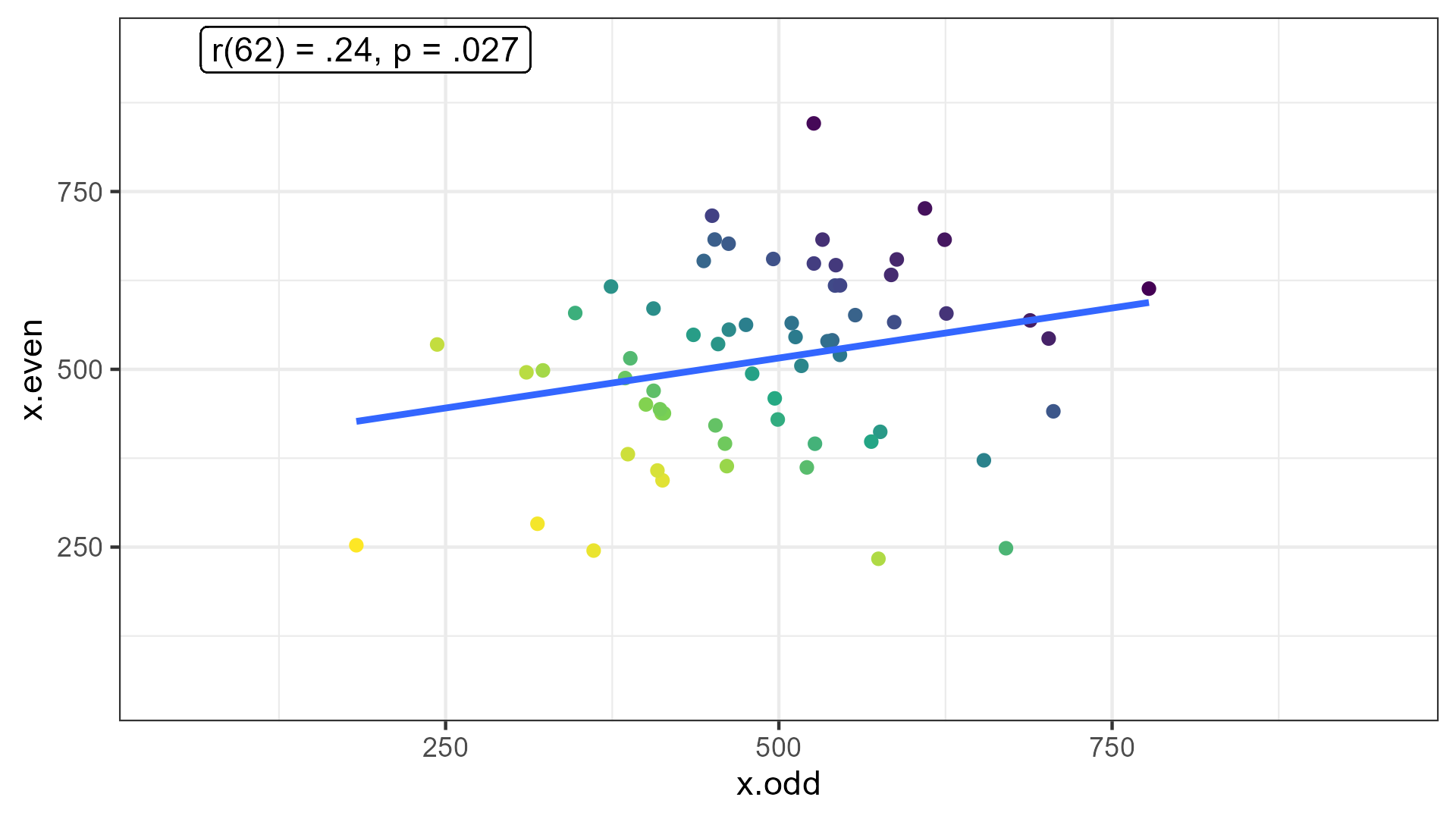
Subject-Level Precision 3

Is there a meaningful correlation?

Simulated data with added noise. True score correlation r = 1 ⇒ We want to enable you to create plots like this one

Side note:
Individual errorbars = subject-level precision of each individual (across trials)
Confidence band of regression slope = group-level precision of the regression estimate (cf. reporting CI around Pearson’s r)

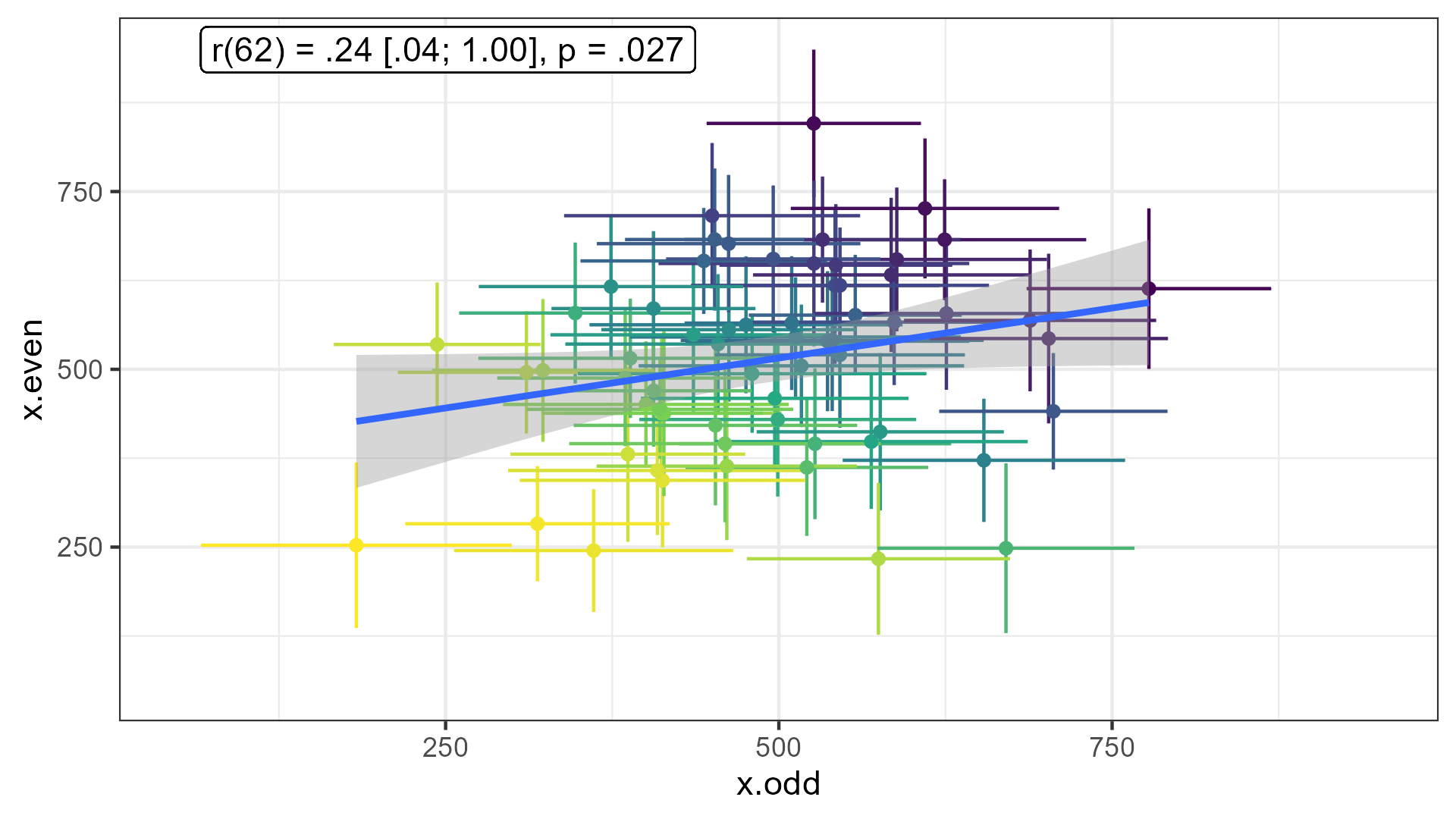
What is Precision? 2

1. Precision is indicated by errorbars / confidence intervals

2. Whenever you summarize across a variable, you can calculate the
   precision of the aggregation

Trial-Level Precision

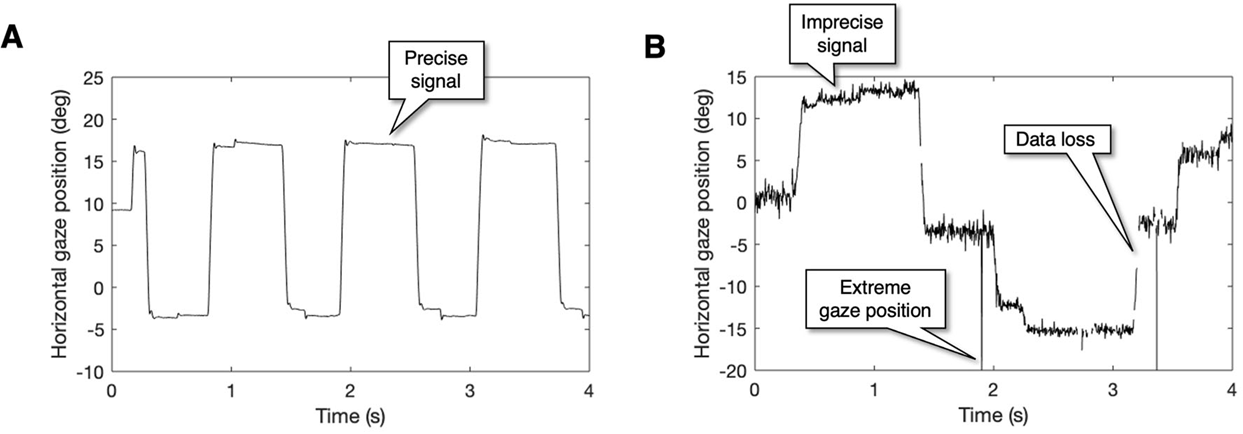
Holmqvist et al. (2023, retracted)

Only relevant for time series data (i.e., several “measurements” per trial)

Note: Calculating standard deviation / error is not trivial here because of auto-correlation

What is Precision? 3

1. Precision is indicated by errorbars / confidence intervals

2. Whenever you summarize across a variable, you can calculate the
   precision of the aggregation

3. Precision exists on different levels: group, subject, trial (and more)

“group” is a very superficial term since you can have nested groups:
classes in schools in cities in districts in countries, etc.

Related Concepts

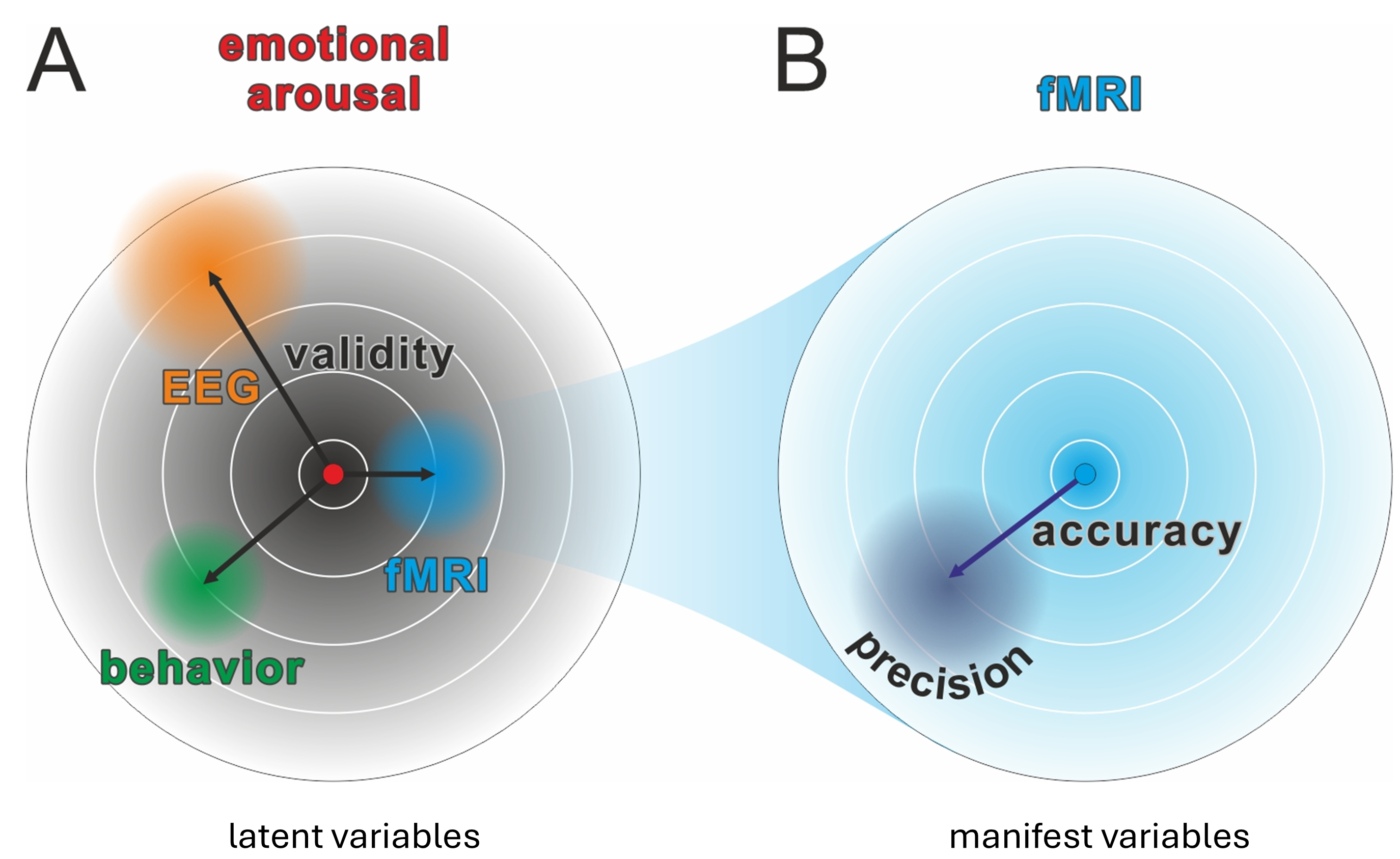
cf. Nebe, Reutter, et al. (2023); Fig. 1

validity: latent (“theoretical”) match between

example for accuracy: systematic bias (miscalibration) in eye tracking

since criterion validity uses a comparison of two manifest variables, this approach can be used to quantify accuracy (absolute agreement) and precision (consistency)

Precision vs. Accuracy

https://www.reddit.com/r/OTMemes/comments/6am425/obiwan_was_right_all_along/

What is Reliability?

Not this!

http://highered.blogspot.com/2012/06/bad-reliability-part-two.html

Where is Reliability highest?

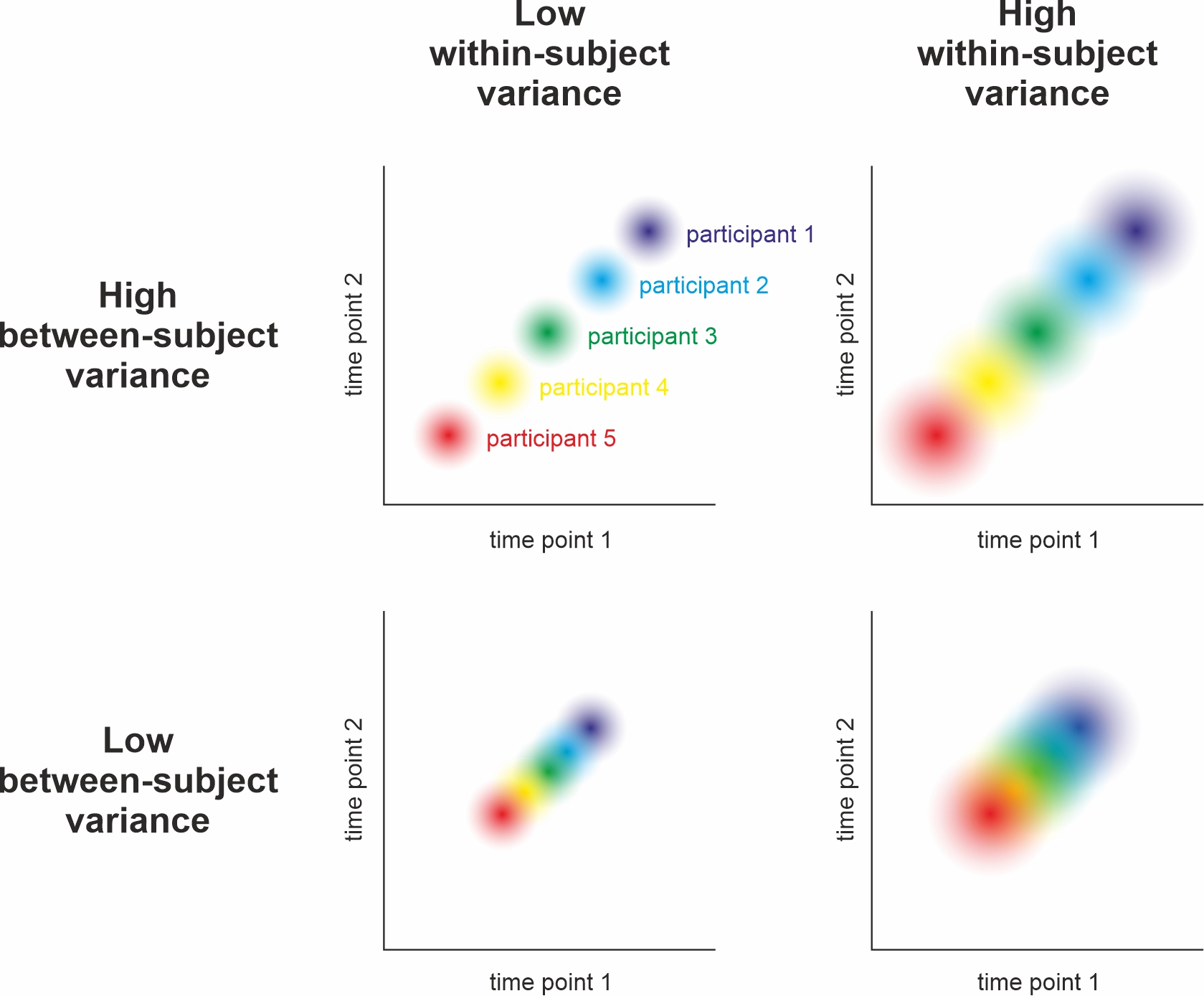
cf. Nebe, Reutter, et al. (2023); Fig. 2

What is Reliability? 2

(Intraclass) Correlation
→ explained variance:
\(R^2 = between / (between + within)\)

Reliability tells you if (to what extent) you can distinguish between low and high trait individuals.

⇒ Reliability =
low subject-level variability (high precision) +
high group-level variability (low precision!)

cf. Nebe, Reutter, et al. (2023); Fig. 2

Spread of bullet holes is precision, not reliability.

Reliability is a COMPOUND MEASURE of high subject-level precision (i.e., low of within-subject variability) plus high between-subject variability (i.e., low group-level precision)
⇒ signal-to-noise ratio with
between = signal & within = noise

Note: Lack of precision does not automatically mean error variance! It can also be due to true score changes.

Reliability Paradox

• Paradigms that produce robust results often show low reliability (Hedge et al., 2018)

• Why do statistical significance and reliability not go hand in hand?

Reliability Paradox

• Paradigms that produce robust results often show low reliability (Hedge et al., 2018)

• Why do statistical significance and reliability not go hand in hand?

  • Statistical power is enhanced by high group-level precision,
    reliability by high group-level variability (cf. previous slide)

  • More subjects only increase group-level precision (high power), leaving subject-level precision constant
    → sample size has no effect on the magnitude of reliability

Reliability vs. Group-Level Precision

• Group-level precision ⇔ homogenous sample / responses

• Reliability ⇔ heterogenous sample / responses

→ Choosing your paradigm and sample, you can optimize for group-level significance OR reliability

Basic research favors different things than (clinical) application (or individual differences research)
⇒ Most of the time group-level precision gets optimized at the cost of reliability

Of course, optimizing group-level significance by using homogenous samples is not good scientific practice

Trial-Level Precision to the Rescue!

Improving trial-level precision of the measurement benefits both subject- and group-level precision
⇒ Nested hierarchy of precision

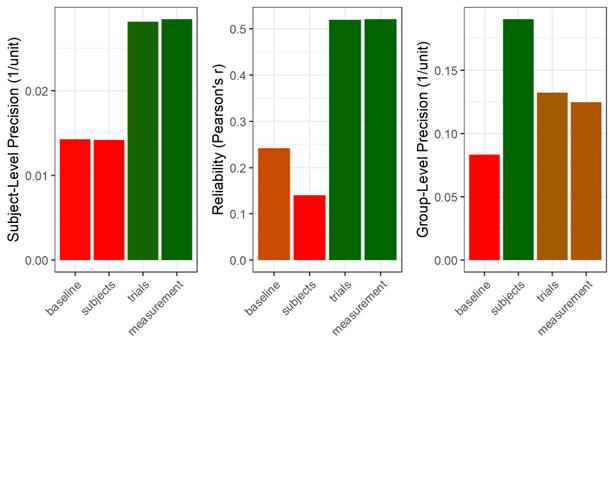
cf. Nebe, Reutter, et al. (2023); Fig. 7

Trial-Level Precision to the Rescue!

Improving trial-level precision of the measurement benefits both subject- and group-level precision
⇒ Nested hierarchy of precision

cf. Nebe, Reutter, et al. (2023); Fig. 7

Summary: What is Precision?

1. Precision is indicated by errorbars / confidence intervals

2. Whenever you summarize across a variable, you can calculate the
   precision of the aggregation

3. Precision exists on different levels: group, subject, trial (and more)

4. Closely linked to statistical power and reliability

How Can We Enhance Precision?

1. Shield the measurement from random noise → precise equipment / paradigm
   ⇒ trial-level precision

2. Identify the aggregation level of interest:

   1. sample differences → optimize group-level precision:
      many subjects that respond homogenously
   2. correlational hypotheses / application → optimize subject-level precision:
      systematic differences between individuals but little variability within subjects across many trials (mind “sequence effects”; cf. Nebe, Reutter, et al., 2023)

⇒ “two disciplines of scientific psychology” (Cronbach, 1957)

Group- vs. Subject-Level Precision

Group-level Precision

• Group differences (t-tests, ANOVA)

• Many subjects (independent observations)

• Homogenous sample (e.g., psychology students?)

Subject-level Precision

• Correlations (e.g., Reliability)

• Many trials (careful: sequence effects!)

• Heterogenous/diverse sample

• Low variability within subjects across trials (i.e., SD_within)

Take Home Message

• We are in a replication crisis

• Increasing the number of subjects is not the only way to get out

• Sample size benefits basic research on groups only

⇒ Increase precision on the aggregate level of interest!

Precision in R!

The Standard Error (SE)

Calculates the (lack of) precision of a mean based on the
standard deviation (\(SD\)) of the individual observations and their number (\(n\))

\[SE = \frac{SD}{\sqrt{n}}\]

The Standard Error (SE) in R

No base R function available 💩

1. Use confintr::se_mean (not part of the tidyverse)

2. Use a custom function

se <- function(x, na.rm = TRUE) {
  sd(x, na.rm) / sqrt(if(!na.rm) length(x) else sum(!is.na(x)))
}

Careful with custom functions! I often see people using n() but this does not work correctly with missing values (NA / na.rm = TRUE)

The Standard Error (SE) in R 2

Whenever you use mean, also calculate the SE:

library(tidyverse)

iris %>% #helpful data set for illustration
  summarize( #aggregation => precision
    across(.cols = starts_with("Sepal"), #everything(), #output too wide
           .fns = list(mean = mean, se = confintr::se_mean)),
    .by = Species)

     Species Sepal.Length_mean Sepal.Length_se Sepal.Width_mean Sepal.Width_se
1     setosa             5.006      0.04984957            3.428     0.05360780
2 versicolor             5.936      0.07299762            2.770     0.04437778
3  virginica             6.588      0.08992695            2.974     0.04560791

→ subject-level (species-level) precision

Standard Error Pitfalls in R

What is the group-level precision of Sepal.Length?

Note: Treat Species as subjects and rows within Species as trials.

data <-
  iris %>% 
  rename(subject = Species, measure = Sepal.Length) %>% 
  mutate(trial = 1:n(), .by = subject) %>% 
  select(subject, trial, measure) %>% arrange(trial, subject) %>% tibble() #neater output
print(data)

# A tibble: 150 × 3
   subject    trial measure
   <fct>      <int>   <dbl>
 1 setosa         1     5.1
 2 versicolor     1     7  
 3 virginica      1     6.3
 4 setosa         2     4.9
 5 versicolor     2     6.4
 6 virginica      2     5.8
 7 setosa         3     4.7
 8 versicolor     3     6.9
 9 virginica      3     7.1
10 setosa         4     4.6
# ℹ 140 more rows

Standard Error Pitfalls in R

What is the group-level precision of Sepal.Length?

data %>% 
  summarize(m = mean(measure),
            se = confintr::se_mean(measure))

# A tibble: 1 × 2
      m     se
  <dbl>  <dbl>
1  5.84 0.0676

data %>% 
  summarize(m = mean(measure),
            se = confintr::se_mean(measure),
            n = n())

# A tibble: 1 × 3
      m     se     n
  <dbl>  <dbl> <int>
1  5.84 0.0676   150

Standard Error Pitfalls in R 2

What is the group-level precision of Sepal.Length?

data %>% 
  summarize(measure.subject = mean(measure), .by = subject) %>% #subject-level averages
  summarize(m = mean(measure.subject),
            se = confintr::se_mean(measure.subject),
            n = n())

# A tibble: 1 × 3
      m    se     n
  <dbl> <dbl> <int>
1  5.84 0.459     3

⇒ When using trial-level data to calculate group-level precision, summarize twice!

⇒ Every summarize brings you up exactly one level - don’t try to skip!
trial-level → subject-level → group-level

Linear Mixed Models (LMMs) implicitly take this into account when specifying random intercepts for subjects (1|subject).

Summary: Precision in R

data %>% 
  summarize(.by = subject, #trial- to subject-level
            measure.subject = mean(measure), #subject-level averages
            se.subject = confintr::se_mean(measure)) %>%  #subject-level precision
  summarize(m = mean(measure.subject), #group-level mean ("grand average")
            se = confintr::se_mean(measure.subject), #group-level precision
            se.subject = mean(se.subject), #average subject-level precision (note: pooling should be used)
            n = n())

# A tibble: 1 × 4
      m    se se.subject     n
  <dbl> <dbl>      <dbl> <int>
1  5.84 0.459     0.0709     3

Thanks!

Learning objectives:

• Learn about the core concept of precision and how it relates to similar constructs (e.g., validity, reliability, statistical power)

• Recognize your aggregate level of interest for research questions and how you can improve its precision

• (Understand the reliability paradox and its relation to precision)

• Calculate precision in R (on different aggregation levels)

Next:

Confidence Intervals