2.2 Confidence Intervals

Workshop: “Handling Uncertainty in your Data”

Dr. Mario Reutter & Juli Nagel

CIs around means

Data preparation

  • If you haven’t done so yet: Create an R project for the precision workshop.
  • Create a script for this part of the workshop (e.g., cis.R).
  • Load the tidyverse (library(tidyverse)) at the beginning of your script.

Note: We show different packages that help us with confidence interval calculations, some of which may have conflicting functions. This is why in this presentation, we call each package explicitly, e.g., confintr::ci_mean().

Why confidence intervals?

  • Goal: indicate precision of a point estimate (e.g., the mean).
  • If visualized, it’s often supposed to help with “inference by eye”.
  • However, confidence intervals are often misinterpreted (e.g., Hoekstra et al., 2014)

What is a confidence interval?

  • Assume we use a 95% CI.
  • In the long run, in 95% of our replications, the interval we calculate will contain the true population mean.
  • As with any statistical inference: no guarantee! Errors are possible.
  • “If a given value is within the interval of a result, the two can be informally assimilated as being comparable.” (Cousineau, 2017)

Confidence interval of the mean


\(M - t_{\gamma} \times SE_{M}, M + t_{\gamma} \times SE_{M}\)


  • \(M\) = mean of a set of observations
  • \(SE_{M}\) = standard error of the mean
  • \(SE_{M} = s/\sqrt n\)
  • \(t_{\gamma}\) = multiplier from a Student \(t\) distribution, with d.f. \(n - 1\) and coverage level \(\gamma\) (often 95%)

Briefly: The iris data

Data about the size of three different species of iris flowers.

head(iris)
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

In R: Confidence interval of the mean

The package confintr offers a variety of functions around confidence intervals. Default here: Student’s \(t\) method.

iris %>% 
  filter(Species == "versicolor") %>% 
  pull(Petal.Width) %>% 
  confintr::ci_mean()

    Two-sided 95% t confidence interval for the population mean

Sample estimate: 1.326 
Confidence interval:
    2.5%    97.5% 
1.269799 1.382201

Also available: Wald and bootstrap CIs.

Confidence interval of the mean


\(M - t_{\gamma} \times SE_{M}, M + t_{\gamma} \times SE_{M}\)


  • However: very “limited” CI!
  • Comparison to a fixed value (e.g., population mean).
  • Cannot easily be used to compare different means.
  • Useless to compare means of repeated-measures designs.

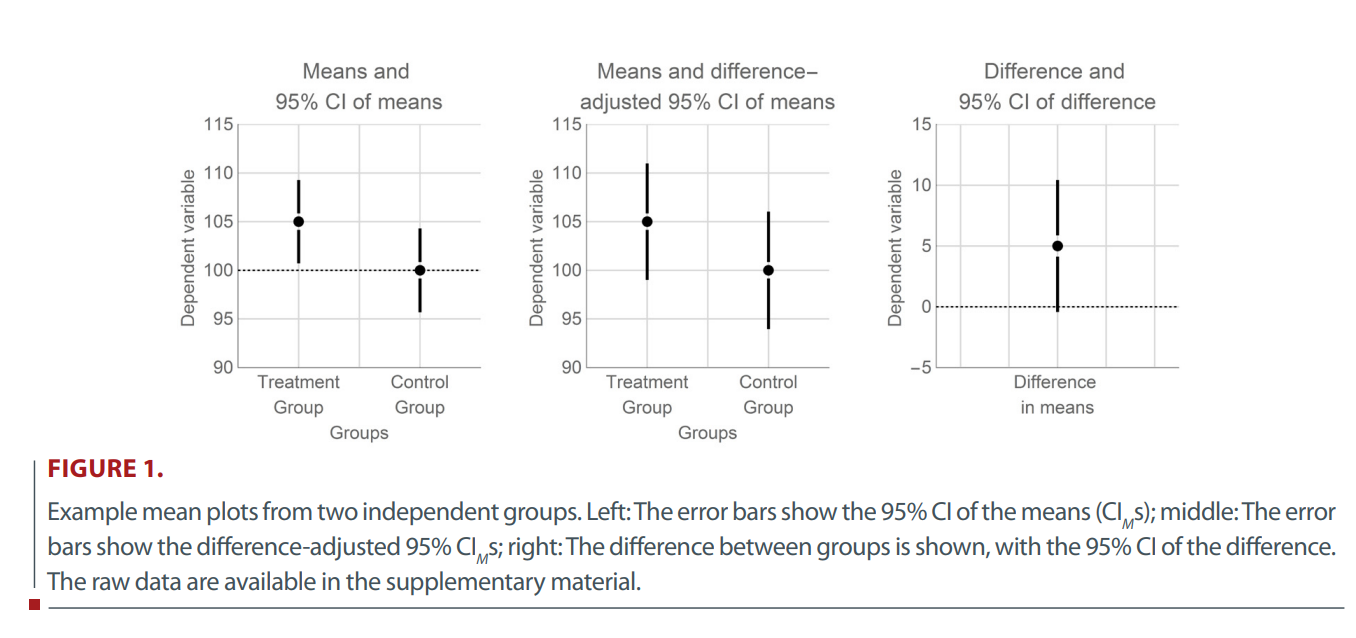
CIs: comparing groups

  • Position of each group mean as well as the relative position of the means are uncertain.
  • I.e., SE for the comparison between two means is larger than for the comparison of a mean with a fixed value.
  • How much the CI needs to be expanded depends on the variance of each group.
  • When the variance is homogeneous across conditions, there is a shortcut: The sum of two equal variances can be calculated by multiplying the common variance by two.
  • I.e., the CI must be \(\sqrt2\) (\(\approx\) 1.41) times wider (\(SE_{M} = \sqrt{Var_{SEM}}\)).


\(M - t_{\gamma} \times \sqrt2 \times SE_{M}, M + t_{\gamma} \times \sqrt2 \times SE_{M}\)

CIs: potential problems when comparing groups

See Cousineau, 2017 - more about data viz later!

In R: custom function

  • Sometimes, writing your own custom function gives you the control you need over certain calculations.


# You've seen this in the previous part :-)
se <- function(x, na.rm = TRUE) {
  sd(x, na.rm) / sqrt(if(!na.rm) length(x) else sum(!is.na(x)))
}


# CI based on t distribution
z_CI_t <- function(x, CI, na.rm = FALSE) {
  if (na.rm) x <- x[!is.na(x)]
  ci <- qt(1 - (1 - CI) / 2, length(x) - 1) # two-sided CI
  return(ci)
}

In R: custom function - applied


iris %>% 
  filter(Species %in% c("setosa", "versicolor")) %>% 
  summarise(
    ci_lower = mean(Petal.Width) - se(Petal.Width) * z_CI_t(Petal.Width, .95),
    ci_upper = mean(Petal.Width) + se(Petal.Width) * z_CI_t(Petal.Width, .95),
    .by = Species
  )
     Species  ci_lower  ci_upper
1     setosa 0.2160497 0.2759503
2 versicolor 1.2697993 1.3822007

CIs: comparing groups

iris %>% 
  filter(Species %in% c("setosa", "versicolor")) %>% 
  summarise(
    ci_lower = mean(Petal.Width) - se(Petal.Width) * sqrt(2) * z_CI_t(Petal.Width, .95),
    ci_upper = mean(Petal.Width) + se(Petal.Width) * sqrt(2) * z_CI_t(Petal.Width, .95),
    .by = Species
  )
     Species  ci_lower  ci_upper
1     setosa 0.2036439 0.2883561
2 versicolor 1.2465202 1.4054798


  • Attention! Assumes equal variance!
  • Even though here, we use the mean and SD/SE of each group (not e.g. the pooled SD).

CIs: difference of means

  • If possible, the most elegant way is to report/plot the CI for the difference in means.
with(
  iris,
  confintr::ci_mean_diff(
    Petal.Width[Species == "versicolor"],
    Petal.Width[Species == "setosa"]
  )
)

    Two-sided 95% t confidence interval for the population value of
    mean(x)-mean(y)

Sample estimate: 1.08 
Confidence interval:
    2.5%    97.5% 
1.016867 1.143133
  • Not pipe-friendly, if that’s important for you.
  • Careful! Not for within-subjects comparisons!

CIs: difference of means

  • Looks familiar? Part of the t.test() output by default!
with(
  iris,
  t.test(
    Petal.Width[Species == "versicolor"],
    Petal.Width[Species == "setosa"]
  )
)

    Welch Two Sample t-test

data:  Petal.Width[Species == "versicolor"] and Petal.Width[Species == "setosa"]
t = 34.08, df = 74.755, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 1.016867 1.143133
sample estimates:
mean of x mean of y 
    1.326     0.246

CIs: difference of means

  • Looks familiar? Part of the t.test() output by default!
  • Can be accessed like this:
ttest_between <- 
  with(
    iris,
    t.test(
      Petal.Width[Species == "versicolor"],
      Petal.Width[Species == "setosa"]
    )
  )

ttest_between$conf.int[1:2]
[1] 1.016867 1.143133

What about within-subject designs?

  • Repeated measures are typically correlated, which makes it possible to evaluate the difference between means more precisely.
  • I.e., we adjust the width of the CI based on the correlation between measures.
  • The difference between the two means is estimated as if we had a larger (independent) sample.


\(M - t_{\gamma} \times \sqrt{1-r} \times \sqrt2 \times \frac{s}{\sqrt{n}}, M + t_{\gamma} \times \sqrt{1-r} \times \sqrt2 \times \frac{s}{\sqrt{n}}\)

Note that we still are comparing two means, so as before, the CI is “difference adjusted” using \(\sqrt2\).

Briefly: the fhch2010 data

  • Data from Freeman, Heathcote, Chalmers, & Hockley (2010), included in afex.
  • Lexical decision and word naming latencies for 300 words and 300 nonwords.
  • For simplicity, we’re only interested in the task (word naming or lexical decision; between subjects) and the stimulus (word or nonword).
library(afex)

head(fhch2010)
  id   task stimulus density frequency length   item    rt      log_rt correct
1 N1 naming     word    high       low      6 potted 1.091  0.08709471    TRUE
2 N1 naming     word     low      high      6 engine 0.876 -0.13238919    TRUE
3 N1 naming     word     low      high      5  ideal 0.710 -0.34249031    TRUE
4 N1 naming  nonword    high      high      5  uares 1.210  0.19062036    TRUE
5 N1 naming  nonword     low      high      4   xazz 0.843 -0.17078832    TRUE
6 N1 naming     word    high      high      4   fill 0.785 -0.24207156    TRUE
# Aggregate to get a word/nonword reaction time per participant
fhch2010_summary <- 
  fhch2010 %>% 
  summarise(rt = mean(rt), .by = c(id, task, stimulus))

CIs for within-subject designs

The measures are highly correlated :-)

fhch2010_summary_wf <- 
  fhch2010_summary %>% 
  pivot_wider(
    id_cols = id,
    names_from = stimulus,
    values_from = rt
  )

fhch2010_summary_wf %>% 
  rstatix::cor_test(word, nonword)
# A tibble: 1 × 8
  var1  var2      cor statistic        p conf.low conf.high method 
  <chr> <chr>   <dbl>     <dbl>    <dbl>    <dbl>     <dbl> <chr>  
1 word  nonword   0.8      8.67 5.40e-11    0.658     0.884 Pearson

CIs for within-subject designs

# without adjusting
fhch2010_summary %>% 
  summarise(
    ci_lower = mean(rt) - se(rt) * sqrt(2) * z_CI_t(rt, .95),
    ci_upper = mean(rt) + se(rt) * sqrt(2) * z_CI_t(rt, .95),
    .by = stimulus
  )
  stimulus  ci_lower ci_upper
1     word 0.8119932 1.056787
2  nonword 0.9912777 1.206521
# adjust for correlation
word_cor <- cor.test(fhch2010_summary_wf$word, fhch2010_summary_wf$nonword)

fhch2010_summary %>% 
  summarise(
    ci_lower = mean(rt) - se(rt) * sqrt(1 - word_cor$estimate) * sqrt(2) * z_CI_t(rt, .95),
    ci_upper = mean(rt) + se(rt) * sqrt(1 - word_cor$estimate) * sqrt(2) * z_CI_t(rt, .95),
    .by = stimulus
  )
  stimulus  ci_lower ci_upper
1     word 0.8793337 0.989447
2  nonword 1.0504891 1.147310

CIs for differences in means in within-subject designs

As before, the \(t\)-test will give us a CI for the difference in means:

with(
  fhch2010_summary,
  t.test(
    rt[stimulus == "word"],
    rt[stimulus == "nonword"],
    paired = TRUE
  )
)

    Paired t-test

data:  rt[stimulus == "word"] and rt[stimulus == "nonword"]
t = -6.2944, df = 44, p-value = 1.245e-07
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -0.2171825 -0.1118359
sample estimates:
mean difference 
     -0.1645092 
# can be accessed using $conf.int[1:2]!

CIs: caveats

  • Assumptions: normally distributed means, homogeneity of variances, sphericity (repeated measures)
  • Mixed designs: Difficult! You will probably need to choose between between-subject or within-subject CIs (depending on your comparisons of interest); see upcoming data viz part!
  • Most importantly: Be transparent! Describe how you calculated your CIs and what they are for!

CIs around effect sizes

Cohen’s d

  • Also possible to report CIs on effect size estimates; different methods of calculating the desired CIs for different measures exist (beyond the scope of this workshop).
  • E.g., cohens_d() from the package effectsize: “CIs are estimated using the noncentrality parameter method (also called the ‘pivot method’)”; see further details at
    ?effectsize::cohens_d().
with(
  iris,
  effectsize::cohens_d(
    Petal.Width[Species == "versicolor"],
    Petal.Width[Species == "setosa"]
  )
)
Cohen's d |       95% CI
------------------------
6.82      | [5.78, 7.83]

- Estimated using pooled SD.

rstatix: pipe-friendly t-test

  • rstatix offers pipe-friendly statistical tests, and also calculates CIs.
  • detailed = TRUE will give us confidence estimates for our \(t\)-test.


iris %>% 
  filter(Species %in% c("setosa", "versicolor")) %>% 
  rstatix::t_test(Petal.Width ~ Species, detailed = TRUE) %>% 
  select(contains("estimate"), statistic:conf.high) #reduce output for slide
# A tibble: 1 × 8
  estimate estimate1 estimate2 statistic        p    df conf.low conf.high
     <dbl>     <dbl>     <dbl>     <dbl>    <dbl> <dbl>    <dbl>     <dbl>
1    -1.08     0.246      1.33     -34.1 2.72e-47  74.8    -1.14     -1.02

rstatix: pipe-friendly Cohen’s d

  • Also includes a pipe-friendly version of Cohen’s d.
  • Careful: CIs are bootstrapped (hence the small discrepancy to the output of effectsize earlier)


iris %>% 
  filter(Species %in% c("setosa", "versicolor")) %>% 
  rstatix::cohens_d(Petal.Width ~ Species, ci = TRUE)
# A tibble: 1 × 9
  .y.         group1 group2     effsize    n1    n2 conf.low conf.high magnitude
* <chr>       <chr>  <chr>        <dbl> <int> <int>    <dbl>     <dbl> <ord>    
1 Petal.Width setosa versicolor   -6.82    50    50    -8.31     -5.95 large

Correlations: apa

Option 1: Using the apa package.


iris %>% 
  summarise(
    cortest = cor.test(Petal.Width, Petal.Length) %>% 
      apa::cor_apa(r_ci = TRUE, print = FALSE),
    .by = Species
  )
     Species                          cortest
1     setosa r(48) = .33 [.06; .56], p = .019
2 versicolor r(48) = .79 [.65; .87], p < .001
3  virginica r(48) = .32 [.05; .55], p = .023

Correlations: rstatix

Option 2: Using the rstatix package.


iris %>% 
  group_by(Species) %>% 
  rstatix::cor_test(Petal.Width, Petal.Length) #implicitly ungroups the data
# A tibble: 3 × 9
  Species    var1       var2    cor statistic        p conf.low conf.high method
  <fct>      <chr>      <chr> <dbl>     <dbl>    <dbl>    <dbl>     <dbl> <chr> 
1 setosa     Petal.Wid… Peta…  0.33      2.44 1.86e- 2   0.0587     0.558 Pears…
2 versicolor Petal.Wid… Peta…  0.79      8.83 1.27e-11   0.651      0.874 Pears…
3 virginica  Petal.Wid… Peta…  0.32      2.36 2.25e- 2   0.0481     0.551 Pears…

Note: Only gives rounded values …

ANOVAs

aov_words <- 
  aov_ez(
    id = "id", 
    dv = "rt", 
    data = fhch2010_summary, 
    between = "task", 
    within = "stimulus",
    # we want to report partial eta² ("pes"), and include the intercept in the output table ...
    anova_table = list(es = "pes", intercept = TRUE)
  )

aov_words
Anova Table (Type 3 tests)

Response: rt
         Effect    df  MSE          F  pes p.value
1   (Intercept) 1, 43 0.10 904.33 *** .955   <.001
2          task 1, 43 0.10  15.76 *** .268   <.001
3      stimulus 1, 43 0.01  77.24 *** .642   <.001
4 task:stimulus 1, 43 0.01  31.89 *** .426   <.001
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1

CI around partial eta²

In principle, apaTables offers a function for CIs around \(\eta_p^2\) …

# e.g., for our task effect
apaTables::get.ci.partial.eta.squared(
  F.value = 15.76, df1 = 1, df2 = 43, conf.level = .95
)
$LL
[1] 0.06851017

$UL
[1] 0.4511011

… but it would be tedious to copy these values.

CI around partial eta²

A little clunky function that can be applied to afex tables:

peta.ci <- 
  function(anova_table, conf.level = .9) { # 90% CIs are recommended for partial eta² (https://daniellakens.blogspot.com/2014/06/calculating-confidence-intervals-for.html#:~:text=Why%20should%20you%20report%2090%25%20CI%20for%20eta%2Dsquared%3F)
    
    result <- 
      apply(anova_table, 1, function(x) {
        ci <- 
          apaTables::get.ci.partial.eta.squared(
            F.value = x["F"], df1 = x["num Df"], df2 = x["den Df"], conf.level = conf.level
          )
        
        return(setNames(c(ci$LL, ci$UL), c("LL", "UL")))
      }) %>% 
      t() %>% 
      as.data.frame()
    
    result$conf.level <- conf.level
    
    return(result)
  }

CI around partial eta²

The result of custom function that applies the apaTables function to our entire ANOVA table:

peta.ci(aov_words$anova_table)
                      LL        UL conf.level
(Intercept)   0.92985360 0.9656284        0.9
task          0.09399555 0.4224818        0.9
stimulus      0.48335736 0.7294335        0.9
task:stimulus 0.23280549 0.5584355        0.9

Also see this blogpost by Daniel Lakens from 2014 about CIs for \(\eta_p^2\).

Thanks!

Learning objectives:

  • Understand what different versions of CIs exist, and which one you need for your data.
  • Apply different functions in R (and write custom ones if needed) to report CIs around means, and common effect size estimates.

Next: Visualizing uncertainty